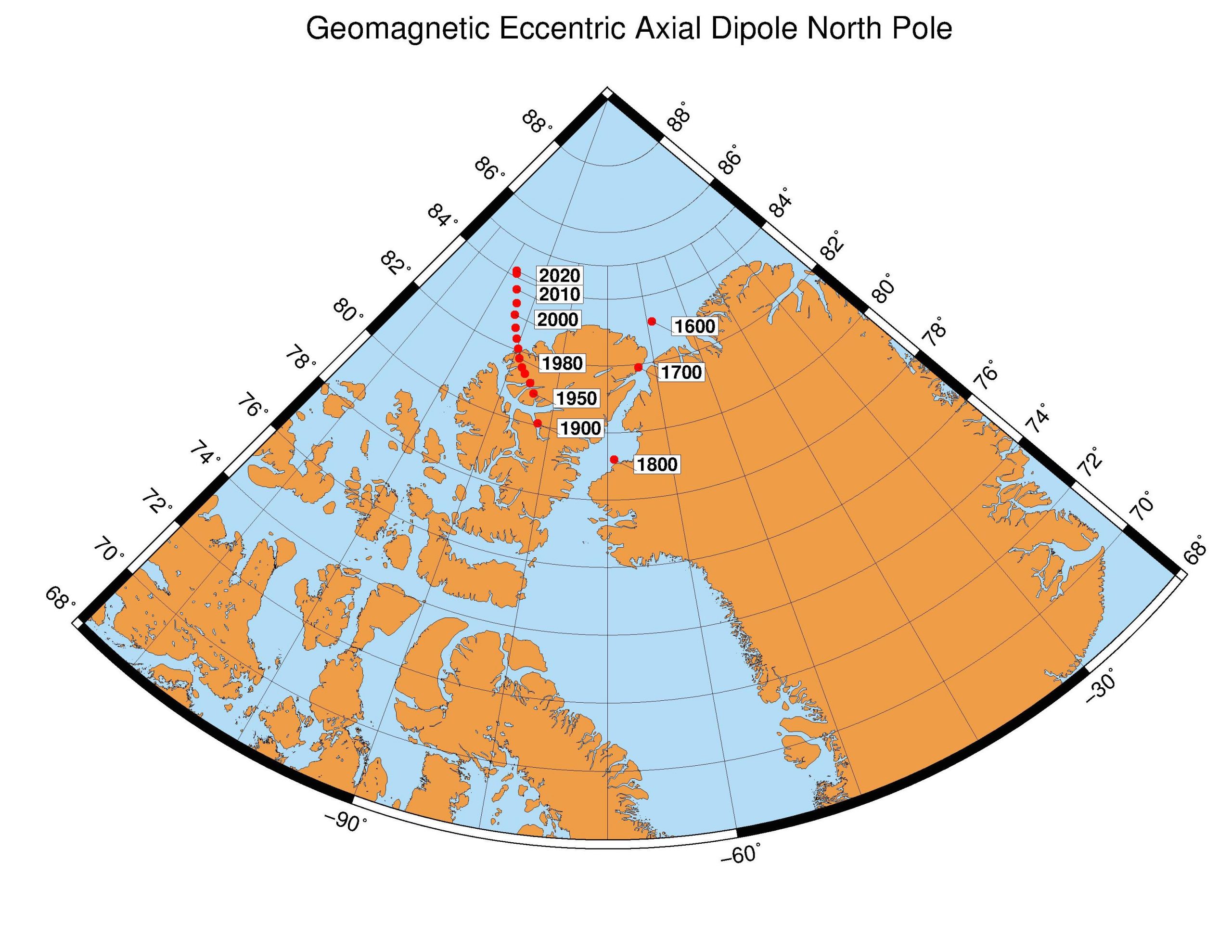
The Eccentric Dipole Model
The Eccentric Dipole (ED) model of Earth's magnetic field is an attempt to get a better approximation Earth's geomagnetic pole locations compared to the simple dipole (i.e. bar magnet) approximation of the centered dipole approach. The eccentric dipole approximation acknowledges that the field is slightly offset from the Earth's spin axis although it retains a dipolar character. The eccentric dipole model uses the first 8 terms of the spherical harmonic expansion (i.e. the Gauss coefficients up to degree 2) of the International Geomagnetic Reference Field (IGRF). These are the g10, g11, h11, g20, g21, h21, g22, h22 terms. Two different types of poles can be calculated: an eccentric dipole axial pole which is where the axis of the dipole intersects the Earth's surface and an eccentric dipole 'dip' pole where the field is vertical at Earth's surface. See Fraser-Smith, (1987) for a full explanation. See also background information on spherical harmonics on the Space Environment Information System operated by the European Space Agency.
The following table lists the calculated Eccentric Dipole (ED) axial pole and dip pole locations for the North Magnetic Pole (NMP). Epochs 1600 through 1800 are from Barraclough (1974) the remainder are calculated from the DGRF/IGRF models.
ED Axial Pole | ED Dip Pole | |||
|---|---|---|---|---|
| Year | ED Axial Latitude (°N) | ED Axial Longitude (°E) | ED Dip Latitude (°N) | ED Dip Longitude (°E) |
| 1600 | 83.2 | 301.2 | 82.3 | 267.2 |
| 1700 | 81.9 | 296.5 | 80.6 | 263.3 |
| 1800 | 79.2 | 291.0 | 78.5 | 268.7 |
| 1900 | 80.06 | 277.76 | 81.07 | 241.07 |
| 1950 | 80.90 | 275.85 | 82.39 | 224.31 |
| 1960 | 81.17 | 274.67 | 82.64 | 218.93 |
| 1970 | 81.40 | 273.18 | 82.70 | 214.25 |
| 1975 | 81.56 | 272.26 | 82.67 | 211.67 |
| 1980 | 81.78 | 271.19 | 82.65 | 208.11 |
| 1985 | 82.05 | 270.20 | 82.65 | 204.24 |
| 1990 | 82.31 | 269.16 | 82.65 | 200.33 |
| 1995 | 82.60 | 268.02 | 82.64 | 200.91 |
| 2000 | 82.96 | 266.97 | 82.68 | 205.53 |
| 2005 | 83.30 | 265.93 | 82.71 | 209.75 |
| 2010 | 83.67 | 264.37 | 82.66 | 213.84 |
| 2015 | 84.09 | 262.43 | 82.52 | 218.56 |
| 2020 | 84.17 | 262.01 | 82.48 | 219.38 |
Like the Centered Dipole (CD) model, the Eccentric Dipole (CD) model of the geomagnetic field is only an approximation of the geomagnetic field using a limited number of the coefficients in the spherical harmonic expansion of the IGRF model. However, these dipole models do give a general sense of the time averaged behavior of the field. It is possible to use all of the Gauss coefficients of the spherical harmonic expansion to define the field and pole locations.
References
Barraclough, D.R., Spherical harmonic analyses of the geomagnetic field for eight epochs between 1600 and 1910, Geophys. J. R. Astron. Soc., 36, 497-513, 1974.
Fraser-Smith, A.C., Centered and Eccentric Geomagnetic Dipoles and their poles, 1600-1985, Rev. Geophys., 25, 1-16, 1986.